Recall that we have shown in a previous post how to colorize 3D shapes with CPPNs.
The basic idea is to assign an RGB color value to each point on the surface of a 3D mesh with a CPPN.
As implied by the word “mesh”, that work heavily relied on the classical and widely used polygon-based rasterization pipeline (common in modern computer games, for example). Specifically, we used the OpenGL bindings for Python to achieve our rendering goal once the color for each model vertex was computed with a CPPN.
Using external rendering libraries (OpenGL) is not as elegant as having everything built from scratch. An option along this path is to use ray tracing (nice tutorials here and here). Note that this option also works perfectly fine for 3D polygonal models (meshes) once you implement a triangl-ray intersection routine.
However, we are going to use sphere tracing [1].
With this approach we can easily compute which pixels belong to the surface of some mathematically defined 3D object (through its signed distance estimator) and then apply CPPN-based colorization as explained in our previous post.
The following pseudocode shows the basic approach for an object defined by sdf_fun:
for m in range(0, M):
for n in range(0, N):
# compute the ray for our current pixel
R = ray_for_pixel(m, n)
# compute the intersection world coordinates
(x, y, z) = find_intersection(R, sdf_fun)
# resulting color for pixel (m, n)
(r, g, b) = apply_cppn(x, y, z)
For speed reasons, we vectorize the above code and implement some parts in C: run.py and tracer.c. Example results are below.
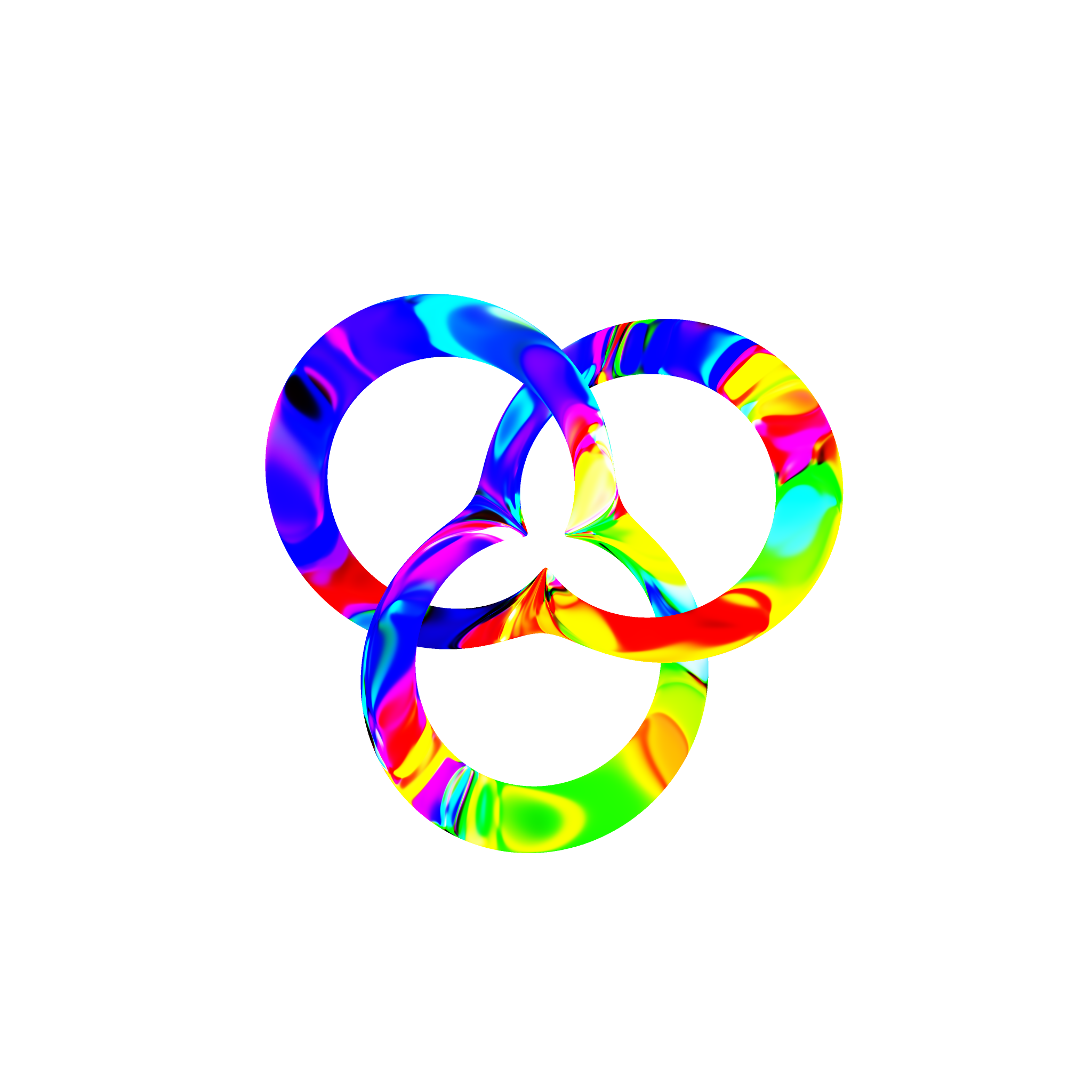
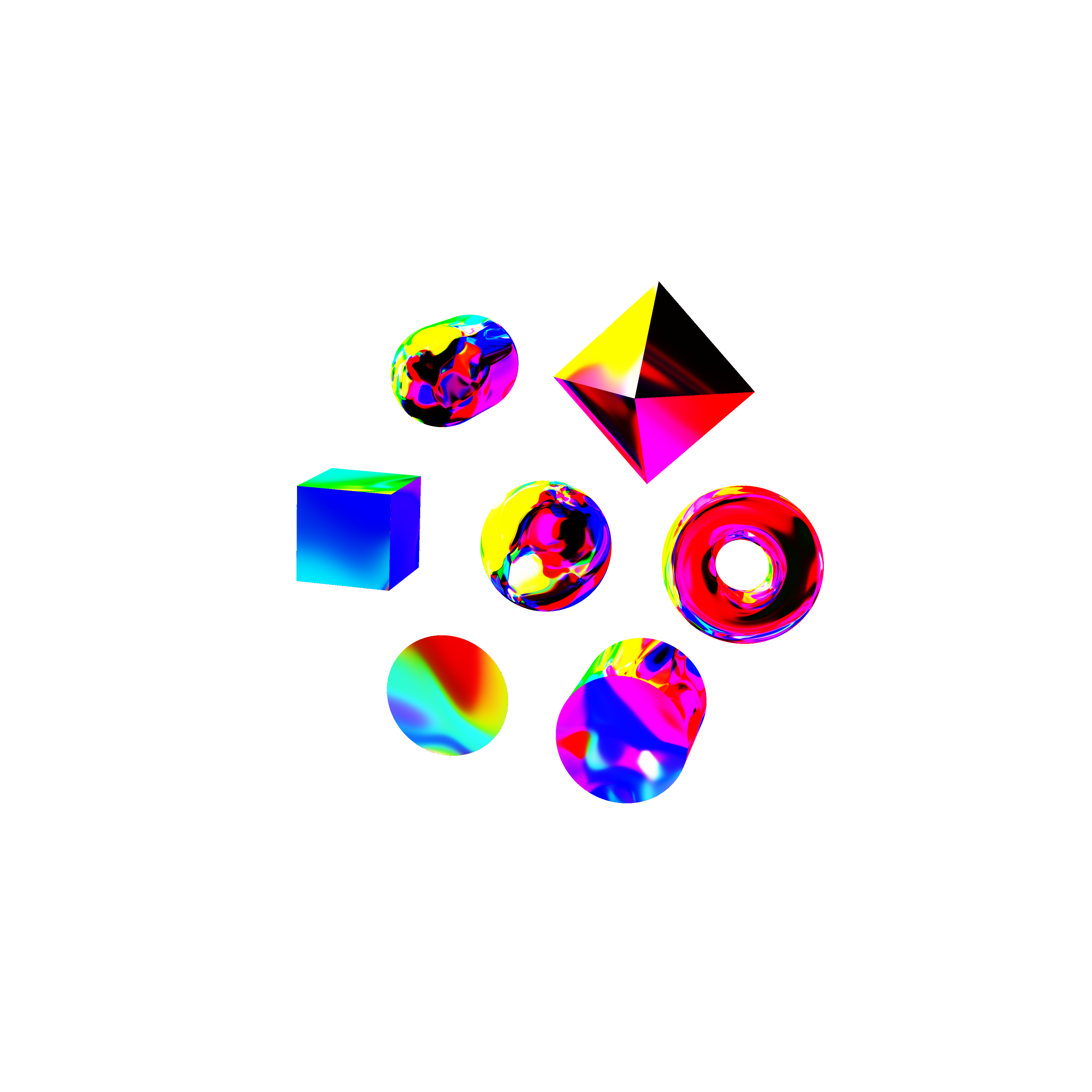
The generate your own, run python3 run.py with tracer.c in the same folder.
[1] J. C. Hart. Sphere tracing: A geometric method for the antialiased ray tracing of implicit surfaces. The Visual Computer, 1994.